O texto a seguir é uma obra Prof. Oscar Matsuura, pesquisador e professor aposentado do Depto. de Astronomia da USP, sobre o trânsito de Mercúrio.
O PRÓXIMO TRÂNSITO DE MERCÚRIO
Oscar T. Matsuura
Professor Associado aposentado do IAG/USP
Pesquisador Colaborador do MAST/MCTIC
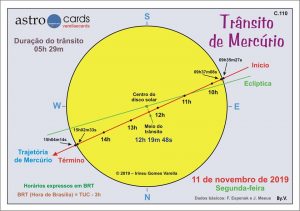
Será no dia 11/11/2019. Uma diminuta mancha escura cruzará quase diametralmente o brilhante disco solar. Quase diametralmente porque Mercúrio passará a apenas 1,3’ do centro do disco solar. O diâmetro da mancha escura será de apenas 0,17’, enquanto o do disco solar será de 32,2’. A trajetória será de SE para NO, desviando-se da direção L-O cerca de 17º.
O trânsito começa quando Mercúrio ingressa no disco solar. Nesse instante, tecnicamente chamado I Contato, o bordo do pequenino disco de Mercúrio toca o bordo externo do disco solar. Cerca de 1,5 minuto depois, o bordo de Mercúrio tocará o bordo interno do disco solar (II Contato). A travessia de Mercúrio por todo o disco solar durará cerca de 5,5 horas. Então, no III Contato o bordo de Mercúrio tocará o bordo interno do disco solar e, cerca de 1,5 minuto depois, no IV Contato, o bordo de Mercúrio tocará o bordo externo do disco solar encerrando o trânsito.
Em relação a esse trânsito, nós brasileiros de todos os cantos do país podemos nos considerar privilegiados! É que o trânsito ocorrerá quando estaremos na parte do globo voltada para o Sol, assim poderemos observar o trânsito. Além disso, segundo os cálculos, o auge do trânsito (quando Mercúrio passará mais perto do centro do disco solar) ocorrerá às 12h 19m 48s no fuso de Brasília, horário esse bem próximo do meio-dia local, quando o Sol em seu movimento diurno encontra-se mais alto no céu. Isso significa também que o início (I Contato) e o fim do trânsito (IV Contato) ocorrerão com o Sol bem elevado em relação aos horizontes L e O, respectivamente, oferecendo as mais favoráveis condições de observação de todo o trânsito, excluindo-se obviamente os fatores meteorológicos.
As condições são privilegiadas também em termos de latitude, pois favorecem o Hemisfério Sul. Assim, em torno do Brasil toda a América do Sul compartilhará também dessas condições. Já, mais a O (p. ex., parte ocidental dos Estados Unidos) se poderá observar só a parte final do trânsito e, mais a L (África, p. ex.), só a parte inicial.
Num texto como este, é meu dever chamar a atenção do leitor para que todo o cuidado seja tomado com os olhos, nunca se olhando diretamente para o Sol (muito menos com algum instrumento), mesmo que brevemente. As lesões que isso pode causar na retina podem ser irreversíveis e causar até cegueira. Adultos devem estar atentos com as crianças sob sua responsabilidade. Sem a assistência direta de um astrônomo experiente, o mais seguro é observar o trânsito projetado num anteparo ou imagens de vídeo transmitidas.
Como ocorre um trânsito?
Estamos o tempo todo num ponto da superfície da Terra, mas o tempo todo a Terra, ao mesmo tempo que gira, orbita ao redor do Sol. Assim, só dois planetas podem se intrometer na nossa linha de visada ao Sol (reta que une a Terra ao Sol): são os planetas interiores do Sistema Solar, Mercúrio e Vênus. Planetas interiores são aqueles cujas órbitas são internas à órbita da Terra. Portanto, assim como há trânsitos de Mercúrio, também há os de Vênus. Mas isso só faz sentido se esses dois planetas orbitam ao redor do Sol, se não exatamente, ao menos aproximadamente no mesmo plano da órbita da Terra. Discutamos melhor isso.
Segundo a 1ª Lei de Kepler (ver adiante), as órbitas planetárias são curvas fechadas e planas: elipses. Portanto a órbita de cada planeta (com o centro do Sol) pode se acomodar inteiramente num plano. Particularmente a órbita que a Terra percorre ao redor do Sol define um plano no espaço chamado plano da eclíptica.
Para a Terra dar uma volta completa ao redor do Sol, não basta 1 ano trópico (o ano do nosso calendário), mas são necessários uns 20 minutos a mais. Esse ano chama-se ano sideral. A trajetória anual que o Sol descreve na esfera celeste em relação às constelações de fundo, “dá visibilidade” à intersecção do plano da eclíptica acima mencionado, com a esfera celeste e é chamada eclíptica. Fica fácil entender isso se considerarmos que a eclíptica é “traçada” na esfera celeste pelo Sol, que se encontra na extremidade distante da linha de visada. A extremidade próxima encontra-se no centro da Terra, que orbita ao redor do Sol. Essa trajetória anual é adjetivada “aparente” pelos astrônomos porque, na verdade, não se trata de um movimento real do Sol, mas de um efeito resultante do movimento orbital da Terra ao redor do Sol.
A órbita da Terra, como acabamos de ver, jaz exatamente no plano da eclíptica. As órbitas dos demais planetas também constituem planos, mas eles não jazem exatamente no plano da eclíptica, senão aproximadamente. Isso tem uma explicação física. O Sol não se formou isoladamente há 4,6 bilhões de anos, mas concomitantemente com todo o Sistema Solar. Isso resultou do colapso gravitacional de uma nuvem de gás e poeira que deu origem à Nebulosa Solar Primitiva. Como essa Nebulosa tinha uma rotação original, à medida que ela se contraía gravitacionalmente, sua rotação se acelerava. Exemplo clássico dessa Lei de Conservação do Momento Angular é a dançarina que rodopia mais depressa quando encolhe os braços. Na parte central da Nebulosa, o Sol acumulava a maior parte da massa, enquanto um bojo equatorial e, mais tarde, um disco equatorial também se formou. Foi nesse disco que os planetas e também os seus satélites se formaram e nele permanecem até hoje, mesmo passados bilhões de anos. Forças e eventos desagregadores têm ocorrido, mas eles causaram apenas perturbações, sem desfigurar a estabilidade geral.
Os planos orbitais de Mercúrio e de Vênus fazem, respectivamente, um ângulo de 7º e de 3,4º em relação ao plano da eclíptica (o desvio de 7º de Mercúrio é o maior de todos os planetas). Ora, aprendemos em Geometria que a intersecção ou o cruzamento entre dois planos determina uma reta. Entre planos orbitais essa reta é chamada linha dos nodos. Assim, enquanto a Terra orbita ao redor do Sol, duas vezes por ano ela cruza a linha dos nodos de Mercúrio, ou de Vênus, em dois pontos da órbita diametralmente opostos. Nesses cruzamentos é certo que o Sol estará na linha de visada, mas não Mercúrio ou Vênus. Para que Mercúrio ou Vênus também esteja, e assim ocorra um trânsito, uma segunda condição é necessária: Mercúrio ou Vênus deve estar numa configuração chamada conjunção inferior.
Que é conjunção inferior? Imaginemos que o plano do papel seja o plano das órbitas planetárias. Imaginemos o Sol e duas órbitas concêntricas a ele, a menor sendo de um planeta interior (Mercúrio ou Vênus) e a maior, da Terra. Para simplificar, fixemos a Terra num ponto qualquer de sua órbita. Tracemos uma reta unindo a Terra ao Sol. A reta interceptará a órbita do planeta interior em dois pontos, um mais próximo da Terra e aquém do Sol, outro mais distante da Terra e além do Sol. Neste último ponto o planeta estará em conjunção superior, enquanto que no anterior ele estará em conjunção inferior.
A Terra cruza a linha dos nodos de Mercúrio ou Vênus duas vezes por ano e o intervalo de tempo é praticamente um semestre. Nos próximos cem anos os trânsitos de Mercúrio ocorrerão entre 7 e 12 de maio ou entre 7 e 15 de novembro. Essas são as duas épocas do ano em que a Terra cruza a linha dos nodos de Mercúrio. A margem de tolerância de vários dias reflete o fato de que o alinhamento entre a Terra, Mercúrio e o Sol não precisa ser exato. Desvios dentro de um limite não impedem que o trânsito seja observado porque os astros envolvidos não são pontos, mas discos com extensão finita.
Mas conjunções inferiores de Mercúrio ocorrem 3 ou 4 vezes por ano. Mesmo assim os trânsitos de Mercúrio ocorrem apenas 13 ou 14 vezes por século! Os trânsitos de novembro se repetem em intervalos de 7, 13 ou 33 anos, enquanto que os de maio só em intervalos de 13 ou 33 anos. A probabilidade de um trânsito de maio é menor que a de novembro porque, em maio, Mercúrio se encontra numa parte da órbita em que sua velocidade orbital é menor, o que diminui a chance de o planeta cruzar o trecho orbital em que o trânsito pode ocorrer. A variação da velocidade orbital de Mercúrio é pronunciada, consequência da 2ª Lei de Kepler, pois esse planeta tem a mais excêntrica das órbitas. O último trânsito de novembro foi em 8 de novembro de 2006, há 13 anos, e o próximo será em 13 de novembro de 2032 daqui 13 anos. O último de maio foi no dia 9 de maio de 2016 e o próximo no dia 7 de maio de 2049, daqui 33 anos.
Os trânsitos de Vênus são ainda mais raros porque o seu período orbital é maior. Na média ocorrem apenas 2 por século. Eles ocorrem aos pares, com separação de 8 anos, mas os pares estão separados alternadamente por 122 e 125 anos. O próximo trânsito de Vênus ocorrerá somente em 11 de dezembro de 2117.
Arquitetura do Sistema Solar
O famoso astrônomo Johannes Kepler (1571-1630) nasceu numa cidadezinha perto de Stuttgart. Piedoso de índole (estudando Astronomia achava que cumpria o dever de entender e enaltecer as obras do Criador), ingressou na Universidade de Tubinga, reduto da ortodoxia luterana, pretendendo tornar-se pastor. Convencido de que o plano divino do Universo era matemático, empenhou-se no estudo da Matemática para ter a chave da Mente Divina. Em Tubinga Kepler teve a sorte de ter Michael Mästlin (1550-1631) como seu mestre de Astronomia. O ensino tradicional do Sistema Geocêntrico, compatível com a Filosofia de Aristóteles, fazia parte da Astronomia ortodoxa. Mas Mästlin percebeu o talento e interesse de Kepler e ensinou a ele o Sistema Heliocêntrico de Copérnico, um avanço recente publicado em 1543. Apesar de ter sido considerada herética pelo próprio Lutero, pois conflitava com passagens bíblicas, Kepler no seu íntimo logo aderiu a essa teoria por achar que ela correspondia à realidade física. Isso, somado a outras posições tomadas por ele em boa fé, mas que conflitavam com a ortodoxia luterana, levaram seus mestres a aconselharem que desistisse da carreira de pastor e se tornasse professor de Matemática em Graz, atual Áustria. Mas, com o tempo, a intolerância contra ele só aumentou, embora mantivesse sua piedade. Em 1612 acabou sendo excomungado!
Na Astronomia, a questão colocada por ele dizia respeito ao tamanho das órbitas dos planetas. Na época eram 6 os planetas conhecidos (Mercúrio, Vênus, Terra, Marte, Júpiter e Saturno). Kepler associou Saturno à esfera mais externa e os demais planetas a 5 sólidos regulares de Euclides. Na esfera de Saturno ele inscreveu um cubo, mas no interior desse cubo estava inscrito uma segunda esfera (órbita de Júpiter) e assim sucessivamente para os demais sólidos. Kepler conseguiu concordância razoável com os tamanhos relativos das órbitas deduzidos por Copérnico. Esse estudo foi desenvolvido enquanto Kepler lecionava em Graz e os resultados foram publicados em Mysterium Cosmographicum (O Segredo do Cosmo) em 1596. Nessa obra Kepler advogou o heliocentrismo, apontando que essa teoria tinha um poder explanatório maior que o geocentrismo.

Ilustração original das órbitas planetárias de Mysterium Cosmographicum (1596). Fonte: https://videnskab.dk/miljo-naturvidenskab/store-opdagelser-johannes-keplers-planetlove
Kepler enviou um exemplar de Mysterium Cosmographicum para Tycho Brahe (1546-1601), o astrônomo dinamarquês de origem nobre que, com generoso patrocínio do rei Frederico II, construiu o famoso observatório Uraniborg, o equipou com os instrumentos astronômicos mais precisos da época, realizou a observação do Cometa de 1577 derrubando a concepção aristotélica de que os cometas eram corpos da atmosfera terrestre, fez observações sistemáticas e precisas de Marte por cerca de 20 anos, cuja importância mostrarei adiante. Antes, Brahe tinha observado a Supernova de 1572 na constelação de Cassiopeia, que derrubou outra concepção aristotélica equivocada, a de que o céu era imutável. Mas quando Kepler enviou o livro, Brahe já tinha perdido o patrocínio de Frederico II, que falecera, e trabalhava em Praga, a convite do Sacro Imperador Romano, Rodolfo II. Brahe havia escrito para Mästlin à procura de um assistente matemático, e Kepler foi indicado.
Por causa da recatolização imposta autoritariamente na Áustria, Kepler que continuava sendo luterano convicto, seguiu em 1600 para Praga no intuito de lá trabalhar com Brahe. Mas este não era de trato fácil e esse encontro não resultou produtivo. Kepler voltou para Graz, mas aí a Contra-Reforma passou a exigir que Kepler se convertesse ao catolicismo. Ele, então, decidiu mudar-se para Praga. Ocorrendo a morte de Brahe em 1601, Rodolfo II o convidou para ser seu matemático e astrólogo. Contornando obstáculos impostos pelos herdeiros de Brahe, Kepler conseguiu ter o desejado acesso às observações sistemáticas de Marte feitas sob a supervisão de Brahe em Uraniborg.
Lei de Kepler e primeiros trânsitos observados
Analisando essas observações, fazendo pacientemente cálculos tediosos por vários anos (não havia computadores), Kepler chegou a uma conclusão revolucionária. Derrubou o velho mito de que as órbitas dos astros tinham que ser circulares porque tinham que ter a forma geométrica perfeita. O desajuste da órbita observada de Marte ao círculo era da ordem de 8’, mas Kepler tinha a certeza de que os erros observacionais de Brahe eram bem menores (cerca de 3’). Assim, confiante, ele enunciou em 1605 sua 1ª Lei, de que a órbita dos planetas eram elipses.
O modelo heliocêntrico previa a ocorrência de trânsitos com menos ambiguidade que o modelo geocêntrico. Em 1607, em meio a seus estudos, Kepler achou que um trânsito de Mercúrio poderia ocorrer no dia 29 de maio. Como não confiava plenamente nos cálculos apressados que tinha feito, começou a fazer observações desde o dia anterior. Improvisou uma câmara escura (em que a luz não é captada por uma lente, mas por um simples orifício) no porão da casa. Chegou a publicar depois que tinha observado Mercúrio em trânsito no disco solar, mas, de fato, como veio a saber depois, tinha observado uma mancha solar. Manchas solares aparecem na superfície do Sol como formações escuras, pois são mais frias que o restante da superfície solar. Hoje sabemos que elas concentram intensos campos magnéticos, sede de ocorrência de explosões solares, fenômenos súbitos e violentos de emissão de radiação e matéria para o meio interplanetário. A previsão do trânsito estava equivocada e, mesmo que estivesse correta, apenas com a câmara escura Kepler não teria podido observar Mercúrio por ser diminuto demais. Algum componente óptico, no mínimo uma lente, seria necessária. Mas não era só Kepler, ninguém então sabia com que tamanho angular Mercúrio apareceria. O tamanho dos planetas era uma questão muito debatida, mas com base apenas em especulações. Para confundir mais a discussão, o conhecimento sobre a atuação da luz na formação das imagens no nosso olho ainda era rudimentar. Também nessa época, em 1609, Galileu introduziu o uso da luneta na observação astronômica e, em 1611, observou as manchas solares pela primeira vez através de uma luneta. Tudo isso mostra o incrível dinamismo dos estudos astronômicos nesses anos. Mesmo sabendo depois do equívoco cometido, Kepler se deu por muito satisfeito por ter sido, sem querer, o primeiro a ter visto uma mancha solar sem o uso da luneta.
Kepler continuou trabalhando em Praga, mas a situação aí piorou. Em 1611 a cidade virou campo de batalha e nela ocorreu um surto de epidemia. Kepler perdeu um dos filhos e a esposa. A tolerância com os protestantes diminuiu na cidade. Em 1612 Kepler decidiu voltar para a Áustria, desta vez para Linz, onde em 1619 publicou, dentre seus novos estudos, sua 3ª Lei, que seria importantíssima, mais tarde, para a utilidade das observações de trânsitos. Nessa etapa da vida, Kepler sofreu estresse adicional para defender sua mãe, acusada de bruxaria. Em 1626 Linz foi sitiada e Kepler seguiu para Ulm na Alemanha, perto de Stuttgart. Aí ele publicou em 1627 as famosas Tabelas Rudolfinas (catálogo estelar e tabelas planetárias), obra dedicada a Rodolfo II, iniciada com Brahe, a quem, no leito de morte, prometeu finalizar. Nessa obra Kepler incluiu a predição do trânsito de Mercúrio de 7 de novembro de 1631, visível na Europa, e o de Vênus um mês depois, em 7 de dezembro de 1631. Este não seria visível da Europa, mas em função das incertezas no cálculo, Kepler recomendou que também se tentasse observar. A observação do trânsito de Mercúrio deveria ser tentada desde o dia 6 até o dia 8. Mas o tamanho com que Mercúrio apareceria ainda permanecia desconhecido.
Para receber os pagamentos atrasados pela publicação das Tabelas Rudolfinas, Kepler viajou para Regensburg onde adoeceu e acabou morrendo em 15 de novembro de 1630, antes de poder observar os trânsitos que anunciara. Foi sepultado na igreja local que foi destruída na Guerra dos Trinta Anos, portanto nada sobrou de seus restos mortais.
No dia do trânsito de Mercúrio, 7 de novembro de 1631, houve mau tempo em geral na Europa, mas pelo menos três observadores que utilizaram o telescópio tiveram sucesso. A primazia dessa observação foi atribuída ao padre Pierre Gassendi (1592-1655) que estava em Paris e pôde fazer observações intermitentes, aproveitando pequenos intervalos de céu aberto. Pela primeira vez se mediu o diâmetro angular de Mercúrio: dificilmente excedia 20”, o que surpreendeu Gassendi que esperava um diâmetro dez vezes maior, da ordem de 1/10 do diâmetro do Sol. Podemos perguntar: por que essa expectativa estava tão errada? Tanto heliocentristas quanto geocentristas imaginavam para a órbita de Saturno um tamanho cerca de 10 mil vezes menor do que o real. Isso fazia supor que todos os planetas estivessem mais perto e que, portanto, deveriam aparecer angularmente maiores. Não foi fácil para Gassendi convencer os mais céticos, que aquele pequeno objeto era Mercúrio. Um argumento a favor foi o movimento de Mercúrio no disco solar. As manchas também se movem devido à rotação do Sol, mas a velocidade é incomparavelmente menor que a de Mercúrio.
Na Europa tentou-se observar o seguinte trânsito de Vênus, de 7 de dezembro de 1631, mas o tempo não ajudou e, quando o céu abria, não foi notada nenhuma mancha escura. Na verdade, na Europa ocidental o trânsito já tinha ocorrido na noite de 6 para 7 e, em Paris, o trânsito já tinha terminado quando o Sol nasceu.
O seguinte trânsito de Vênus em 1639, não foi predito por Kepler porque ele ainda não sabia que esses trânsitos ocorrem aos pares com separação de 8 anos. Melhorando os cálculos de Kepler, o pastor inglês Jeremiah Horrocks (1618-1641) previu o trânsito de 4 de dezembro de 1639 que ele e seu colega da Universidade de Cambridge, William Cabtree (1610-1644) observaram. De sua aldeia ao norte de Liverpool, Horrocks conseguiu observar o início do trânsito, mas logo depois o Sol se pôs. Mesmo assim conseguiu determinar o tamanho angular de Vênus que seria umas 8 vezes maior que o de Mercúrio. Cabtree também observou de sua casa perto de Manchester, mas, sucumbindo à forte emoção, esqueceu-se de fazer qualquer anotação útil. Mas, até aí, ninguém ainda tinha tido a ideia de usar trânsitos para determinar a distância da Terra ao Sol.
Trânsitos e a Unidade Astronômica
A 3ª Lei de Kepler, enunciada em 1609, relaciona matematicamente o período orbital de um planeta com sua distância média ao Sol. Esse é um enunciado de grande utilidade porque o período orbital pode ser medido através de observações feitas da Terra. Conhecendo os períodos orbitais dos planetas do Sistema Solar, essa Lei permite calcular a distância relativa desses planetas ao Sol. Podemos saber quantas vezes um planeta está mais perto do Sol, ou mais longe do que outro. Porém, sabendo a distância absoluta de apenas um planeta, podemos saber a distância absoluta de todos os outros. Como obter uma distância absoluta?
Em princípio, a observação simultânea de um astro feita de duas localidades da superfície da Terra pode fornecer a distância desse astro até a Terra. O método tradicional faz uso do conceito de paralaxe. Esse conceito é simples: apontando o indicador para cima, estique o braço para a frente. Veja esse dedo, alternadamente, só com o olho direito e só com o olho esquerdo. Note que, em relação ao fundo, o dedo se desloca alternadamente para o lado do olho fechado. Neste caso, a linha de base de observação é formada pelos dois olhos, cuja separação é de poucos centímetros. Esse conceito pode ser transportado para distâncias maiores, p. ex., observando de dois lugares separados algumas dezenas de metros (linha de base maior), uma árvore no meio de uma praça. Relativamente à paisagem de fundo, a árvore mudará de direção. Essa mudança aparente da direção de um objeto, quando visto de lugares diferentes, é chamada paralaxe. Esse conceito é usado na Astronomia até mesmo para a determinação da distância de estrelas mais próximas.
A Lua, por ser o astro permanente mais próximo à Terra, tem uma paralaxe da ordem de 1º. Trata-se de uma paralaxe “enorme” pois, mesmo com equipamentos simples, pode ser facilmente medida. Hiparco de Niceia (190 a.C. – 120 a.C.) a mediu no século 2 a.C. O ângulo de deslocamento aparente da Lua, de cerca de 1º em relação às estrelas de fundo, é o que se obteria se a Lua fosse fotografada simultaneamente de dois pontos da superfície da Terra separados 6.370 km (raio da Terra) numa linha de base transversal à linha de visada. É fácil ver que a distância da Lua à Terra resulta de uma conta simples que soluciona um triângulo plano cujos elementos são conhecidos.
Poderíamos pensar em utilizar o mesmo método para determinar a distância do Sol. Teríamos que determinar a paralaxe do Sol. Mas essa já não é uma tarefa trivial. A mesma linha de base equivalente ao raio da Terra torna-se muito pequena relativamente à nova distância entre a Terra e o Sol. Com os conhecimentos atuais, sabemos que a paralaxe do Sol, definida como foi para a Lua, seria de apenas 8,8”, ângulo esse muito pequeno para ser medido com boa precisão, mais ainda tratando-se do Sol. Para começo de conversa, a observação não é noturna, mas diurna quando a atmosfera encontra-se mais turbulenta e instável. Além do brilho excessivo do disco solar, a determinação do centro do disco é dificultada pela agitação caótica da borda. Por isso, ninguém que tentou esse método teve sucesso, e outros métodos tiveram que ser concebidos.
O inglês Edmond Halley (1656-1742), ligado ao famoso cometa cujo retorno periódico às proximidades do Sol ele foi o primeiro a predizer, numa expedição científica à ilha de Santa Helena, no Atlântico Sul, lá fez importantes observações astronômicas, inclusive do trânsito de Mercúrio de 7 de novembro de 1677. Isso o levou a sugerir em 1691 que a duração total de trânsitos de Vênus, que podem ser melhor observados que os de Mercúrio, e que ocorreriam em 1761 e 1769, fosse medida de diferentes lugares da Terra com precisão de 1 s. Sabendo-se a distância entre as órbitas de Vênus e da Terra, já se tinha uma distância absoluta para a aplicação da 3ª Lei de Kepler. Numa época em que ainda não havia relógios de precisão, medir independentemente a duração total de um trânsito de Vênus em dois lugares diferentes era mais fácil do que determinar o horário dos contatos em lugares diferentes. A bem da verdade, o matemático e astrônomo escocês James Gregory (1638-1675), inventor do telescópio refletor gregoriano, já tinha feito, independentemente, sugestão equivalente em 1663.
Mas, em 1672, 5 anos antes da observação de Halley do trânsito de Mercúrio em Santa Helena, Giovanni-Domenico Cassini (1625-1712), primeiro diretor do Observatório de Paris, e Jean Picard (1620-1682) em Paris e Jean Richer (1630-1696) em Caiena, Guiana Francesa, usaram uma outra estratégia para determinar a distância absoluta de Marte à Terra numa configuração planetária especial. Eles tiraram vantagem de uma oposição de Marte (planeta exterior). Quando alinhado com a Terra e o Sol, esse planeta pode ficar bem afastado ou bem próximo da Terra. Neste último caso temos uma oposição, o que favorece a medição da paralaxe. Estando nessa configuração, Marte foi observado simultaneamente de Paris e de Caiena. Usando essa paralaxe e a 3ª Lei de Kepler, pela primeira vez a Unidade Astronômica – distância média do Sol à Terra, isto é, a média aritmética entre as distâncias máxima e mínima entre o Sol e a Terra – teve uma dedução confiável, embora ainda 7% inferior ao valor atual. A calibração absoluta do Sistema Solar é feita com a Unidade Astronômica, cuja abreviação legal estipulada pelo Inmetro (Instituto Nacional de Metrologia, Qualidade e Tecnologia) é “ua”. Em números redondos, 1 ua = 150 milhões km.
Os trânsitos de Vênus de 1761 e 1769 alertados por Halley, foram objeto de uma ampla cooperação internacional, considerada a primeira na História da Astronomia. Os locais para os quais as expedições de diferentes países se deslocaram eram muitas vezes inóspitos, sem nenhuma infraestrutura, implicaram viagens longas e desconfortáveis com doenças, invernos rigorosos e conflitos políticos, inclusive entre os países dos próprios astrônomos expedicionários, como a Guerra dos Sete Anos. A observação do trânsito de Vênus trouxe uma surpresa técnica desagradável, o problema inesperado da gota negra, um efeito óptico quando os bordos de Vênus e do Sol se tocam e parecem se fundir, o que dificulta a determinação precisa dos instantes de contato. Mas, mesmo assim esses trânsitos forneceram valores mais confiáveis da ua, desta vez cerca de 2% acima do valor atual. Os resultados foram melhorados ainda mais com as novas medições nos trânsitos de 1874 e 1882. Para este último, o Imperial Observatório do Rio de Janeiro, atual Observatório Nacional enviou expedições para três localidades distintas: Olinda, PE, Punta Arenas na Patagônia chilena e Ilha São Tomás nas Antilhas.
Posteriormente as medições se tornaram ainda mais precisas com o uso da fotografia e com a observação de asteroides que se aproximam da Terra e, mais recentemente, com o uso de radares e de sinais de rádio. A União Astronômica Internacional adotou 1 ua = 149.597.870,700 km. Notar o último algarismo significativo! De fato, a incerteza atual é da ordem de apenas alguns metros!
Comentários finais
A precisão da ua é importante não só para o conhecimento correto de distâncias no âmbito do Sistema Solar, como também para o conhecimento de distâncias estelares, pelo menos das mais próximas, cujas distâncias são determinadas pelo método da paralaxe tendo por linha de base o diâmetro da órbita da Terra (2 ua). A mesma estrela é observada uma vez e, novamente, seis meses depois quando a Terra se encontra no ponto diametralmente oposto da órbita. Esse método deixa de ser aplicável para estrelas e galáxias mais distantes. Então, novos métodos tornam-se necessários, mas mesmo esses dependem das distâncias mais próximas determinadas com a paralaxe. É nesse sentido que se diz que usamos uma “escada cósmica” para galgar, desde os astros mais próximos até os astros mais distantes do Universo.
Até o final do século passado só se observava trânsitos de planetas do Sistema Solar. Hoje, com telescópios mais sofisticados e poderosos, são observados trânsitos de planetas na frente de outras estrelas, o que constitui, pelo menos neste momento, o método de observação mais produtivo para a descoberta de novos exoplanetas.